|
1 Solución de problemas.
Las cuatro etapas de la resolución de problemas con una computadora se dan a continuación:
1. Entender el problema: un modo de manejar un problema es la de imaginar el tipo de salida que debe producirse para distintas entradas posibles. Después determinar el tipo de proceso necesario para convertir la entrada en salida.
2. Encontrar un método de solución: esto es, diseñar un algoritmo que le permita definir los pasos que llevarán a la solución del problema.
3. Traducir el método a código de computadora: este paso es generalmente sencillo cuando se ha concretado un método paso a paso y se conoce la sintaxis del lenguaje de programación.
4. Probar y depurar: si la ejecución del programa no es la correcta, se deben encontrar y corregir los errores que contenga. Este proceso se llama depuración. Posteriormente debe ejecutarse el programa con una amplia variedad de entradas para verificar que la lógica del programa esté correcta.
2 Algoritmo
Definición de Algoritmo.
La palabra algoritmo proviene del nombre del matemático islámico Abu Jafar Muhamed ibn Musä al Khwàrizm quien murió en el año 847 A.C.
Un algoritmo para un problema es una secuencia de pasos a seguir, no ambiguos, finitos y determinísticos que llevan a la solución de un problema,
Para poder elaborar un algoritmo, es necesario recordar las siguientes observaciones:
1. El algoritmo debe escribirse como una expresión en algún lenguaje:
¨ Descripción narrada
¨ Notación matemática
¨ Pseudocódigo
¨ Diagramas de flujo
¨ Lenguaje de computadora.
2. Exactamente cada pregunta del problema debe ser contestada por la ejecución del algoritmo.
3. Cualquiera que sean los valores de las entradas, la ejecución terminará después de algún número finito de pasos.
Por ello, para que una computadora pueda resolver un problema concreto, el usuario
y no la computadora, debe diseñar un método adecuado para la solución. La computadora
simplemente llevará a cabo paso a paso la lista de las instrucciones formuladas en el
programa del usuario.
3 Técnicas para la descripción de algoritmos.
1. Descripción Narrada. Se utiliza el lenguaje natural ya sea hablado o escrito. Por ejemplo, la receta para hacer un pastel.
2. Notación matemática: se expresa mediante fórmulas matemáticas que determinarán las salidas del problema.
3. Diagramas de flujo: en ésta técnica se utilizan símbolos que representan cada paso de
los algoritmos. Los símbolos más utilizados son los siguientes:
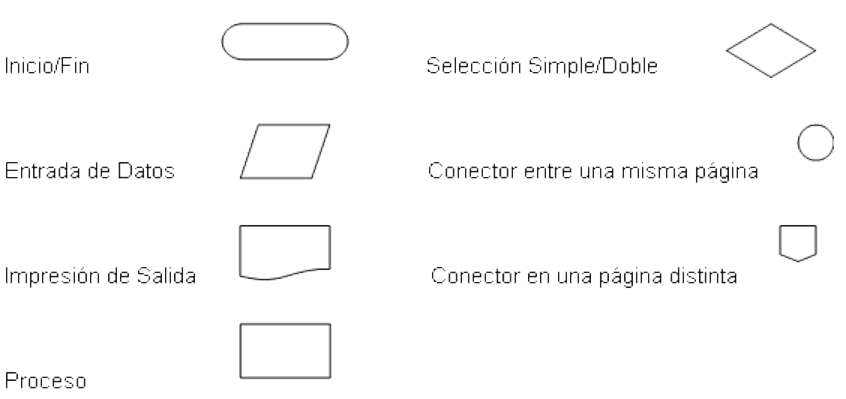 OBSERVACIONES:
a) Es importante conservar los diagramas de flujo lo más sencillo posible, y apoyarse en el significado de la simbología. Por ello, debemos evitar escribir demasiado texto dentro de cada uno de los símbolos, y en su lugar, utilizar sólo el identificador de la variable y las expresiones aritméticas, relacionales o lógicas según sea el caso.
b) Para un buen estilo de diseño del algoritmo, y en general, para ayudar la traducción posterior al lenguaje de programación deseado, es necesario conservar la verticalidad del diagrama, sin inventar conexiones diferentes a las establecidas.
c) Es muy importante utilizar los símbolos adecuados para cada operación a realizar. De esta forma, en el símbolo condicional, no deben incluirse asignaciones; ni en el símbolo de proceso se pueden incluir operadores relacionales ni lógicos.
4. Pseudocódigo: es un lenguaje informal para la descripción de algoritmos, debido a que es muy flexible y depende del estilo del programador. Toma características de un lenguaje de programación y de los procesos matemáticos para detallar el problema. Para ello se deben tomar en cuenta las siguientes reglas:
¨ Los comentarios se denotan con /* */
¨ Se utilizan las estructuras de control de flujo (para, mientras, si)
¨ Asignarle nombres coherentes a las variables, de acuerdo con lo que representan y según el contexto del problema.
¨ Delimitar el inicio y fin del algoritmo y de las estructuras de control de flujo.
4 Tipos de datos.
Una de las tareas principales de la computadora es almacenar y procesar datos. Para
hacer esto, un programa utiliza estructuras de datos, es decir, formas para almacenar los
diferentes datos que van a ser procesados. Conforme aumenta la complejidad del programa,
también será más compleja la forma en que se almacenan estos datos.
La forma más sencilla de almacenar datos en un programa es mediante el uso de
variables y constantes.
Un programa asigna una posición de memoria a cada variable o constante que sea declarada en el programa. La posición en memoria puede ser vista como una casilla de memoria, en donde el valor será determinado por el programa, y el tipo de valor que puede ser almacenado en ella será determinado por el programador al momento de declarar la variable.
Para una variable, el valor en dicha casilla cambiará tantas veces lo necesite en el programa; en cambio, para una constante, su valor es fijado una vez, al, inicio del programa, y no puede cambiar durante el transcurso de éste.
A toda variable o constante se le asigna un nombre o identificador, el cual debe construirse de acuerdo con las siguientes reglas.
1. El identificador debe empezar con una letra, seguida de letras, números o el carácter "_".
2. No se pueden utilizar espacios en blanco
3. No se puede utilizar ningún otro símbolo como #, $, %, /, *, @, etc.
4. Se toma como referencia de longitud máxima de 8 caracteres (aunque algunos lenguajes aceptan hasta 127)
5. El identificador debe tener relación con el problema.
5 Operadores
Los operadores nos permiten realizar operaciones aritméticas entre los datos, ya sean constantes o variables.
Aunque el número y tipo de operadores depende del lenguaje de programación que se esté utilizando, los operadores más frecuentes se clasifican de la siguiente forma:
1. Operadores aritméticos. Los cuales son:
+,-,*, / y el mod, o módulo de la división.
El operador mod sólo se aplica a operandos tipo entero. El mod se lee como módulo de la división, y el resultado será el residuo de una división entera.
2. Operadores de relación Los cuales son:
>, >=, <, <=, !=, ==
Se hace una distinción con el operador de igualdad, que no es el mismo de asignación: ==. Así se tiene x == y se traduce como "¿es x igual a y?, en tanto que x=y, equivale a decir "a la variable x se le asigna el mismo valor que tiene y "
3. Operadores lógicos. Los cuales son:
! (not, negación) && (and, y), || (or, o)
Para resolver expresiones con operadores lógicos, se utilizan las siguientes tablas, conocidas como tablas de verdad:
|
x |
! (NOT) |
|
Falso |
Verdadero |
|
Verdadero |
Falso |
|
x |
y |
&& (AND) |
|
Falso |
Falso |
Falso |
|
Falso |
Verdadero |
Falso |
|
Verdadero |
Falso |
Falso |
|
Verdadero |
Verdadero |
Verdadero |
|
x |
y |
II (OR) |
|
Falso |
Falso |
Falso |
|
Falso |
Verdadero |
Verdadero |
|
Verdadero |
Falso |
Verdadero |
|
Verdadero |
Verdadero |
Verdadero |
4. Operadores de Asignación
Por el momento, el único operador de asignación es: =
Las reglas para resolver una expresión aritmética son las siguientes:
1. Los operadores aritméticos se aplican teniendo en cuenta su jerarquía (precedencia) y de izquierda a derecha. La jerarquía se muestra a continuación:
- (Unario), ! (Not, negación)
() Paréntesis
*, /, mod
<, <=, ==, >, >=, !=,+,- (Resta)
&& (AND)
|| (OR)
=
2. Si una expresión contiene paréntesis, se evalúa primero la subexpresión entre paréntesis, respetando la jerarquía de operadores en esta.
6 Reglas para la elaboración de algoritmos.
- Identificar todas las variables que intervienen en el problema a resolver. Para ello, te puedes auxiliar de una tabla como la que se muestra a continuación:
|
Nombre de la variable |
Posibles valores |
Descripción |
Cómo tomará su valor |
|
|
|
|
|
Una vez que las has identificado, en el algoritmo sólo podrás utilizar el nombre que le has asignado. Cuídate de no cambiarles nombre, ni significado, durante el desarrollo de tu algoritmo.
- Toda variable debe tener un valor, ya sea por que se le solicita como entrada o por que se le asigna dentro del algoritmo.
- Respeta las reglas para la creación de identificadores al momento de crear los nombres para tus variables.
- En el símbolo de proceso, sólo se pueden utilizar los operadores aritméticos (+,-,, *, /, mod) y asignación (=)
- En el símbolo condicional, sólo se pueden utilizar los operadores relacionales (<, <=, >, >=, ==, !=), y los operadores lógicos (AND, OR, NOT ó &&, ||, ! )
Ejem.:
x > z
y==5
Si se trata de una condición compuesta, el formato será:
(variable operador variable/valor) AND/OR (variable operador variable/valor)
- De la misma forma, en el caso de una operación de asignación, su formato será:
variable = variable/valor operador variable/valor
Ejem.:
x = y * 3
7 Estructuras de control de flujo
La verdadera ventaja de utilizar una computadora para la resolución de problemas consiste en su capacidad de procesar un gran volumen de datos a una gran velocidad, permitiéndonos repetir el mismo proceso sobre datos diferentes.
Las estructuras de control de flujo nos permiten tomar decisiones o repetir una secuencia de pasos sobre diferentes datos.
7.1 Estructura de Selección Simple y Doble.
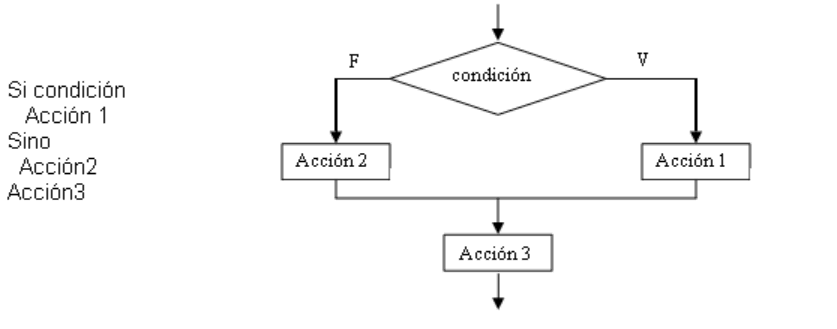
Este tipo de estructura, nos-permite seleccionar entre dos posibles alternativas de acción. Su forma general es:
| Estructura condicional |
|
| Estructura condicional |
En este caso, si la condición es verdadera, se ejecuta la Acción1, si es falsa, se ejecuta la Acción 2. En ambos casos, terminada la estructura, se ejecutará la Acción 3.
Cuando se ejecutan más de una acción en las ramas falsa o verdadera, es necesario delimitar el inicio y el fin de cada rama, de tal forma que el pseudocódigo debe escribirse:
Si condición
Inicio
Acción 1
. /* más acciones */
Fin
Sino
Inicio
Acción2
.. /* más acciones */
Fin
Acción3
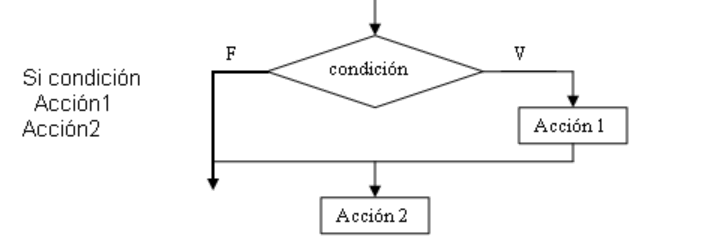
En ocasiones, esta estructura no presenta la rama "Sino", en este caso se tiene una estructura de selección simple:
| Condicional Simple |
|
| Condicional Simple |
OBSERVACIONES:
1. En el símbolo de decisión, (el rombo), sólo deben utilizarse expresiones con operadores aritméticos y/o lógicos.
2. Por consiguiente, en el símbolo de decisión no se puede utilizar el símbolo de asignación.
3. Si se requiere utilizar símbolos aritméticos, es permitido siempre y cuando, se comparen utilizando un operador relacional y no uno de asignación, ejemplo:
z > x+y Correcto
z = x+y Incorrecto
4. Los operadores lógicos se utilizan para unir dos o más condiciones. Por ejemplo:
x>y && y<z
5. El símbolo de decisión o condicional (el rombo) no puede utilizarse para ninguna otra cosa que no sea para tomar una decisión (preguntar). No se pueden leer datos de entrada, ni asignar valores a una variable, ni utilizarlo como símbolo de salida.
6. En un pseudocódigo, si existe una rama Sino, debe existir una rama "Si".
7.2 Estructura de Selección Múltiple.
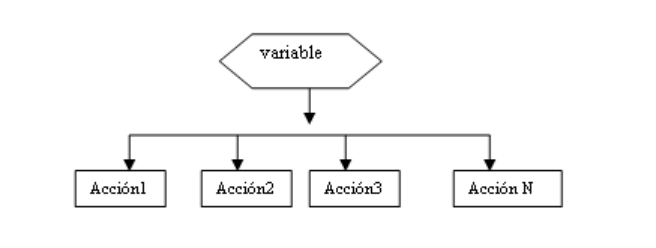
Este tipo de estructura, nos permite seleccionar entre más de dos posibles alternativas de acción. Su forma general es:
Seleccionar variable
Caso opción1: acción1
Caso opción2: acción2
Caso opción3: acción3
Caso opción4: acción4
En otro caso: acción N
| Condicional múltiple |
|
| Condicional múltiple |
7.2 Ciclos.
Una posibilidad poderosa de la computadora es su capacidad de ejecutar el mismo grupo de líneas. Ese el proceso de ciclos, y el grupo de líneas que se ejecutan varias veces se llama el "cuerpo del ciclo".
Un ciclo es ventajoso cuando se ha de repetir esencialmente la misma tarea un número especificado de veces. En tales casos, basta solucionar una sola vez el problema.
Las tres estructuras disponibles para ciclos son: la estructura "para", "mientras" y "hacer".
7.3 Ciclo controlado por contador.
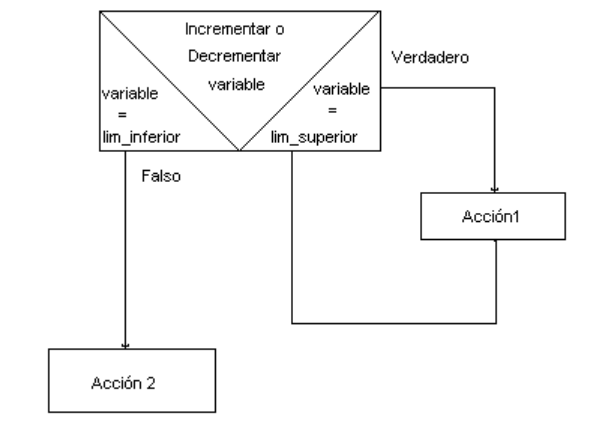
Este ciclo es el más sencillo, ya que se conoce con exactitud cuantas veces se va a llevar a cabo la misma tarea. Una variable (el contador) se incrementa o decrementa, y la acción se ejecuta hasta que la variable llegue al límite superior. Su forma general es:
Para variable = limite_inferior Hasta variable <= limite_superior en Inc/Dec
Acción1
Acción2
| Ciclo controlado por contador |
|
| Ciclo controlado por contador |
De la misma forma que en la estructura condicional, si realiza más de una acción dentro del ciclo, se deben delimitar colocando las palabras inicio y fin.
OBSERVACIONES
A) La variable a utilizar como contador o variable de control, no se le pueden asignar incrementos o decrementos diferentes de 1, es decir, incrementos tipo 2, 4, 6, 8 o incrementos 0, 0.5 1.0, 1.5, etc., no son correctos, por lo que si se tiene un problema de este tipo, se necesitará utilizar una tipo de ciclo diferente.
B) No se debe modificar el valor de la variable de control dentro del cuerpo del ciclo, ya que esto alteraría su valor y por consiguiente, el número de veces que se repetirán las acciones.
7.4 Ciclo "mientras"
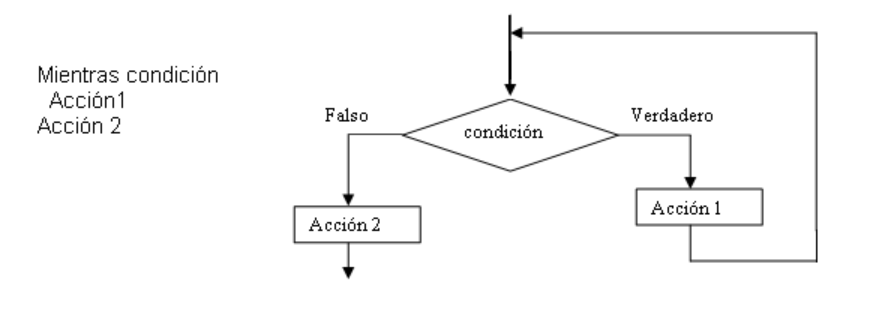
En este ciclo no se conoce con exactitud cuantas veces se va a repetir el proceso. En este caso, la acción se va a llevar a cabo mientras una determinada condición sea verdadera, lo que puede ocasionar que no sea ejecutada ni una sola vez. Su forma general es:
| Ciclo mientras |
|
| Ciclo mientras |
Para formular las condiciones se emplean los símbolos relacionales como >, <, =, etc.
Así trabaja un ciclo "mientras": se prueba la condición, si esta es verdadera, se ejecuta la acción1, y se regresa al principio para volver a probar la condición. Este proceso se repite hasta que la condición sea falsa, en cuyo caso, se ejecuta la acción 2.
OBSERVACIONES:
a) Es necesario comprobar, mediante el uso de la prueba de escritorio, que el ciclo va a tener fin.
b) Se pueden realizar incrementos o decrementos de la variable de control en pasos diferentes de 1, esto es 2,4,6,8, ó 0,2,0.3, 0.4, etc.
c) Si el ciclo depende de una variable de control, ésta debe cambiar su valor dentro del cuerpo del ciclo, a diferencia de lo sucedido con el ciclo para.
d) El ciclo mientras se debe utilizar cuando primero se requiere hacer una comparación, y después repetir un número determinado de acciones.
7.5 Ciclo "Hacer"
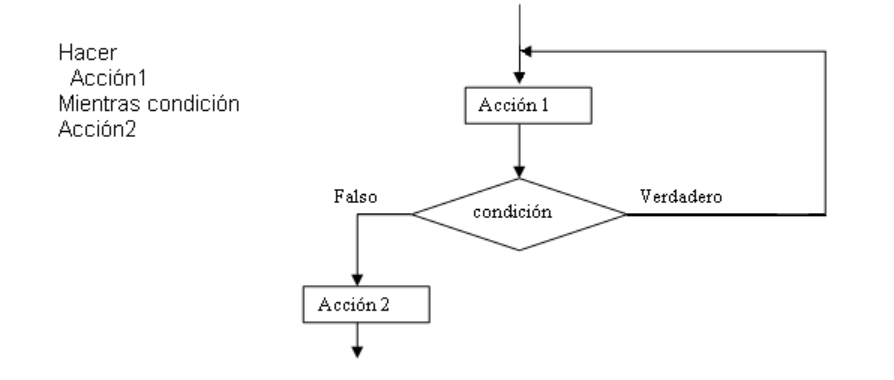
Este ciclo es muy similar al anterior, con la diferencia de que en éste, por lo menos se realiza la tarea una vez. El ciclo "Hacer" primero realiza la acción y después evalúa la condición. Su forma general es
| Ciclo hacer |
|
| Ciclo hacer |
OBSERVACIONES:
e) Es necesario comprobar, mediante el uso de la prueba de escritorio, que el ciclo va a tener fin.
f) Se pueden realizar incrementos o decrementos de la variable de control en pasos diferentes de 1, esto es 2,4,6,8, ó 0,2,0.3, 0.4, etc.
g) Si el ciclo depende de una variable de control, ésta debe cambiar su valor dentro del cuerpo del ciclo, a diferencia de lo sucedido con el ciclo para.
h) El ciclo hacer se debe utilizar cuando primero se requiere hacer un número determinado de acciones y después una comparación para saber si es necesario seguir repitiendo estas acciones.
8. Prueba de escritorio.
La prueba de escritorio también es conocida como trazado del algoritmo, y es muy útil para conocer el valor de salida de un algoritmo, o el comportamiento del mismo.
Elaborar una prueba de escritorio es muy sencillo. Para comenzar el trazado del algoritmo, es necesario crear una tabla, con las variables que intervienen en el algoritmo, e ir colocando su valor conforme cambia en el transcurso del algoritmo. Por ejemplo, para el siguiente pseudocódigo, se tiene la siguiente prueba de escritorio:
Inicio
suma = 0
Para x=1 Hasta x<=3 en Incrementos
suma = suma + x
Imprimir(suma)
Fin
|
suma |
x |
Salida |
|
0 |
1 |
|
|
1 |
2 |
|
|
3 |
3 |
|
|
6 |
4 |
6 |
GNP
|